Chapter 3 — The 14-Dimensional Tapestry
The ancient philosophers imagined that beneath the flux of appearances lay a harmony of number, a geometry whose unseen strings set matter dancing. In the framework of Informational Phase Space Cosmology (IPSC), that intuition proves literal: the universe is not built upon particles scattered in space, but upon correlations woven in a manifold of information. Spacetime is the fabric’s visible shimmer, a projection of a far richer weave — fourteen informational dimensions vibrating in coherence.
To reach this manifold, one begins with quantum structure. Every qubit can be described by three independent observables, represented by the Pauli matrices σx, σy, σz. Each corresponds to a distinct axis of correlation: phase, orientation, and complementarity. But a universe of one qubit has no dialogue; information arises only through relation. The minimal relational system is three qubits, each capable of entanglement with the others. Their pairwise correlators form a nine-dimensional subspace — nine axes along which differences can echo between systems. Add to these the five degrees of freedom that describe how correlations twist, curl, and accumulate memory — the holonomic and entropic dimensions — and we obtain the complete informational manifold I14.
Unlike the 10 or 11 dimensions of string theory, the fourteen of IPSC are not spatial. They are informational directions: gradients along which correlations can vary without contradiction. Some correspond to measurable physical quantities (phase coherence, spin orientation, entropic gradient); others encode purely relational properties, invisible yet indispensable, like grammar hidden behind a poem. When the manifold projects into a lower-dimensional slice — the spacetime we experience — the fourteen coordinates fold into four effective ones: three of space and one of time. The rest become latent variables, contributing curvature and coupling constants the way unseen harmonics color a note.
Mathematically, this projection can be expressed by a mapping π: I14 → M4, where M4 is the emergent spacetime manifold. The induced metric on M4 is obtained by pulling back the informational metric g(info)AB via π, yielding gμν = ∂μπA ∂νπB g(info)AB. What general relativity treats as intrinsic curvature of space is, in this view, the shadow of informational curvature in I14. Gravitational wells are regions where informational flows converge; cosmic expansion is the stretching of correlational distance between sectors of the manifold.
Within I14, curvature and topology acquire new meaning. A closed loop through the manifold — a cycle of correlations returning to their origin — rarely returns unchanged. The mismatch defines holonomy, the memory of informational transport. These loops form the topological memory sectors Mk introduced earlier. Each sector acts as a persistent bias, a cosmic habit acquired through repetition. The presence of such memory may manifest as small anisotropies in the cosmic microwave background, or as rotational signatures in large-scale structure. The universe, like a language that remembers its idioms, cannot speak without its history inflecting every sentence.
Informational vorticity — the curl ΩAB of the informational velocity field vA = ∇ASinfo — plays the role of angular momentum in this manifold. Where vorticity vanishes, the informational flow is irrotational and projects as flat spacetime. Where it persists, we observe cosmic rotation, torsion, and the subtle handedness of nature itself. The left-right asymmetry of weak interactions and the dominance of matter over antimatter may both be linguistic artifacts — grammatical preferences of the universe’s syntax rooted in its informational vorticity.
One can visualize the manifold as a loom. The warp threads are correlations — constraints that run longitudinally through reality. The weft threads are entropic flows — transverse gradients of possibility. At their intersections, curvature arises: each crossing defines a local patch of spacetime. The density of weaving sets the Planck scale; the tension in the threads defines the cosmological constant. Thus the entire observable universe can be understood as a finite cloth woven from informational threads under cosmic tension.
Why fourteen? Because self-reference demands redundancy. A system capable of encoding its own informational state must reserve extra dimensions to represent the relations among relations. Just as a sentence about sentences requires a meta-language, the universe’s capacity to model itself requires meta-dimensions of correlation. Nine suffice to encode all pairwise relations among three entangled systems; five more allow the system to track its own entropy gradients and topological feedback. Beyond fourteen, the structure becomes over-complete; below it, self-reference breaks. The number is therefore not chosen but discovered — the minimal grammar for a self-consistent universe.
The emergent spacetime inherits its metric properties from this projection. The cosmological constant Λ corresponds to the average informational curvature ⟨R(info)⟩, and variations in Λ across epochs represent shifts in how the manifold allocates its degrees of freedom. Dark energy thus ceases to be a mysterious fluid and becomes the elastic response of the informational fabric to expanding complexity. As new patterns form — galaxies, life, mind — the universe adjusts its geometry to preserve coherence, trading curvature for meaning.
This feedback between structure and semantics is what gives IPSC its teleodynamic flavor. The universe is not evolving toward a goal but toward greater self-coherence. Each informational loop that stabilizes adds a new degree of freedom; each degree of freedom allows finer distinctions; and finer distinctions permit new forms of structure. It is an autocatalytic process: information learning to sustain its own meaning. What we perceive as the arrow of time is the direction of that learning — from coarse grammar to refined syntax.
In human language, context gives dimension to words; in the cosmos, correlation gives dimension to space. The three dimensions of ordinary space are the minimal number needed for mutual reference among distinct informational lines; time emerges as the ordering of updates within that network. But beneath the visible geometry runs a deeper grammar of fourteen variables — the complete set of ways information can relate to itself without incoherence. To speak of reality as fourteen-dimensional is not to inflate space, but to admit that being has more grammar than our eyes can parse.
Ultimately, the 14-dimensional tapestry is not a mystical beyond but a scientific necessity. It is the minimal manifold on which information can maintain global consistency while projecting locally as space, time, and matter. Its equations will be developed in later sections: how the Pauli correlator algebra defines its metric, how Fisher information determines its curvature, and how the feedback between entropy and holonomy produces observable phenomena such as cosmic rotation and dark energy. For now, it is enough to see the pattern: reality as a woven text of information, a self-consistent grammar whose syntax we are only beginning to read.
The next chapter turns from the structure of the weave to its function — to how feedback and memory within the informational manifold create a cosmos that can learn, remember, and refine its own laws. There we will encounter the idea of topological memory in depth and see why the universe, in the end, is not a static fabric but a living text — a tapestry still being woven from the threads of meaning itself.
The Geometry of Context
Every structure—physical, linguistic, biological—depends on context for its stability. In the informational universe of IPSC, context itself is geometry: the shape traced by correlations as they curve through phase space. Spacetime does not underlie information; it precipitates from it, a continuous grammar through which distinctions remain self-consistent. This section will dive deeply into the specific structural distinctions that quite literally matter- herein treated as a verb meaning "to make matter [the way it is]". If the details of this section overwhelm you, don't worry- understanding all of the nuts and bolts isn't a prerequisite for comprehending the remainder of this book's content. It is presented here primarily to drive home the point that IPSC is more than useful set of metaphors- it is a bona fide model of the cosmos that can be used to make predictions about the real world. My motivation for choosing jargon (ie, "information") is largely arbitrary. It is rooted in past and present uses of the word, to be sure, but nothing about IPSC as a model would have been different had I chosen to call it "Love", "God", or "The Tao", so long as all of the logical, semantic, and mathematical relations remained unchanged. This fact-that no-thing is any-thing until it is related to another thing, and the nature of each thing is only understood through its relations- captures the ontological essence of IPSC-
In this view, curvature and connection are not abstractions but statements about how information flows. The metric tensor gμν emerges as a bookkeeping device for how correlations distribute; its curvature Rμν describes how the second derivatives of those correlations twist through one another. Continuity is smooth context change, topology is looping context, and vibration is rhythmic feedback—the manifold speaking in its own meter.
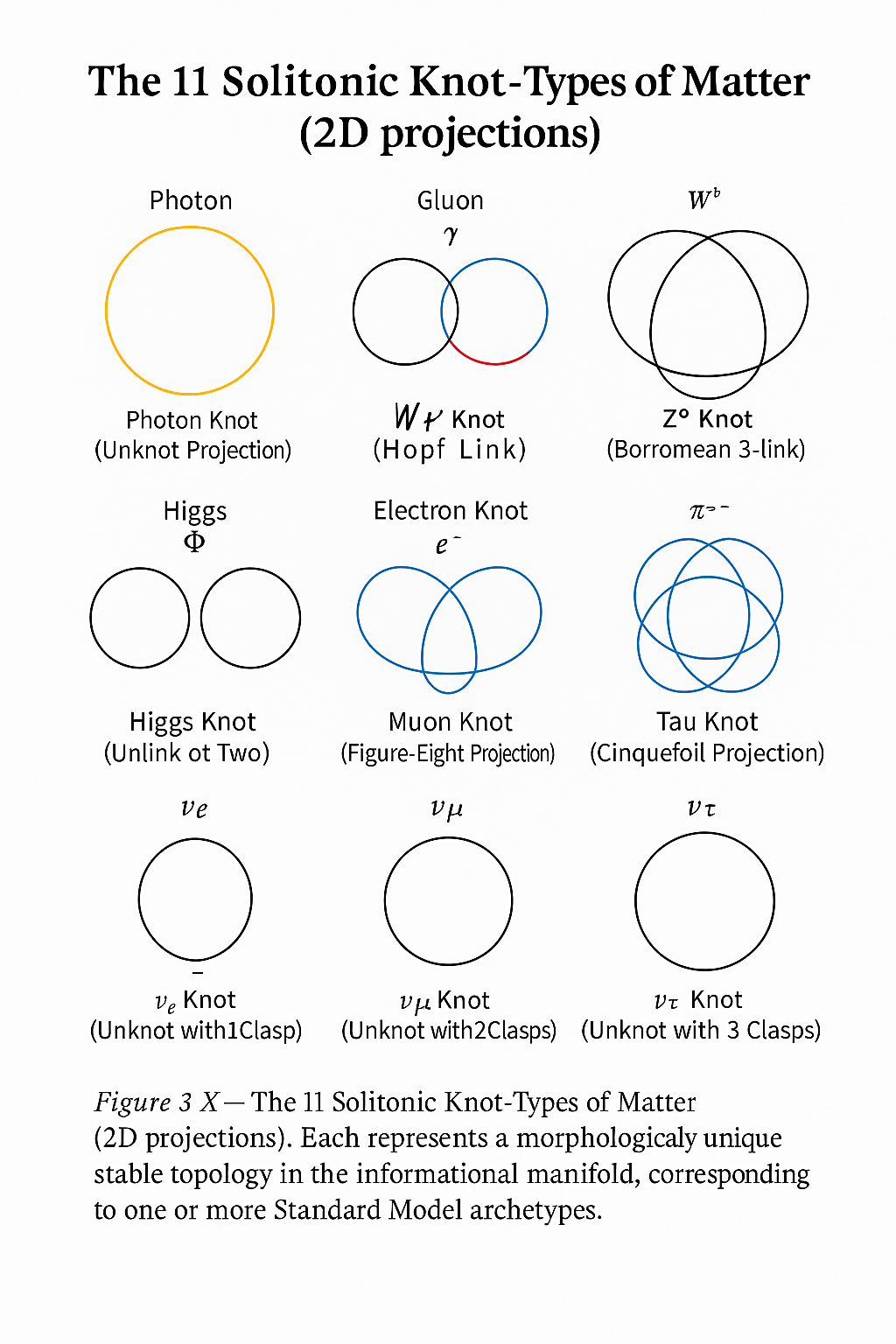
The Seventeen Solitonic Knot-Types of Matter
The same principles that shape large-scale curvature also sculpt the micro-architecture of matter. When informational fields become locally self-referential, they tie themselves into stable knots—solitonic patterns that neither dissipate nor diverge. In IPSC, what particle physics calls “fields” and “quanta” are the topologically distinct, dynamically stable knots of the informational manifold.
Detailed analysis of the IPSC field equations identifies exactly seventeen topologically stable knot-types, each corresponding to one of the fundamental species of the Standard Model. These include the gauge bosons, the Higgs excitation, and three generations of leptons and quarks. The mapping is not symbolic but geometric: each knot type represents a different solution class of the informational curvature tensor, stabilized by distinct combinations of helicity, linking number, and phase holonomy.
Classification Overview
| Sector | Representative Fields | Topological Invariants | Informational Signature |
|---|---|---|---|
| Gauge Bosons | g, γ, W±, Z0 | Linking number = 0 or ±1 Twist parity = even | Pure curvature loops; propagate context synchrony across the manifold. |
| Higgs Mode | Φ | Null linking; self-knot of genus 1 | Scalar fold stabilizing local information density minima; sets coherence scale for mass. |
| Leptons (3 generations) | νe,μ,τ, e, μ, τ | Twist number ±1⁄2; chirality encoded in handed loop orientation | Single-strand closed loops with phase defects; carry informational charge analogous to electric Q. |
| Quarks (3 × doublets) | u, d / c, s / t, b | Triple-braid links with color holonomy SU(3) | Knots with threefold branching; braid phase defines color charge and confinement. |
Mapping to Quantum Numbers
Each knot-type possesses a unique set of informational invariants that correspond directly to the Standard Model’s quantum numbers: spin J, SU(3) and SU(2) representations, hypercharge Y, and electric charge Q. The Quantum Numbers Table developed in the IPSC laboratory papers lists these correspondences explicitly. For reference, the pattern can be summarized schematically:
| Informational Topology | Physical Interpretation | Standard Model Analog |
|---|---|---|
| Simple loop (0 link) | Massless propagating curvature | Photon, gluon |
| Linked pair (±1 link) | Broken symmetry rotator | W±, Z0 |
| Folded scalar loop (genus 1) | Vacuum tension stabilizer | Higgs boson |
| Single chiral loop with phase defect | Left/right handed fermion | Leptons (e, μ, τ and neutrinos) |
| Three-braid link with SU(3) holonomy | Color triplet field | Quarks (u, d, c, s, t, b) |
The Standard Model enumerates states of excitation—61 total when generations, charges, and antiparticles are included (48 fermions and 13 bosons). IPSC, in contrast, enumerates informational morphologies: the topologically distinct, dynamically stable knots that generate those excitations. Only 17 stable knot-types exist in the informational manifold, and of these, 11 possess topologically unique two-dimensional projections.
Many Standard-Model “particles” differ not by topology but by parameterization—variations in curvature tension, coupling constant, or holonomy phase—so that entire families (for example, all quark flavors or all charged leptons) share a single solitonic form. The figures in the original IPSC soliton paper therefore depict archetypal geometries, not a one-to-one correspondence with the 61 observed excitations. In IPSC, the manifold’s 17 knot-types are the alphabet from which the universe composes every physical “word.”
Informational stability corresponds to topological conservation: a solitonic knot can only transform into another of equal topological charge through high-energy reconnection events. This conservation replaces the arbitrary “quantum number assignments” of traditional particle physics with geometric necessity.
Why Seventeen?
The IPSC field equations, when projected onto the minimal 14-dimensional informational manifold, yield seventeen distinct equivalence classes of solitonic curvature under the allowable gauge transformations. Each class minimizes informational action under one of the possible symmetry embeddings of SU(3) × SU(2) × U(1). Beyond these seventeen, knots either destabilize (radiating into curvature waves) or collapse (merging with the informational vacuum). The finitude of this set explains why matter appears in discrete families rather than as a continuum of excitations.
Later chapters will explore how these knots interact through curvature exchange, how their informational holonomy drives cosmic asymmetries, and how their topology underlies the emergence of meaning itself in complex systems.
Thus the geometry of context, first encountered as a description of space and time, extends downward into the micro-fabric of existence. Each stable pattern of curvature is a syllable of reality’s language—seventeen solitonic vowels and consonants from which the manifold composes the text of the world.